|
|
|
Premier
cadran
analemmatiques
Voici donc le premier type de cadran répondant au problème. Il se caractérise par une direction de projection parallèle à l'équateur. Le cercle auxiliaire projeté se réduit alors à un segment de droite. La figure 1 représente le cercle auxiliaire (A) de centre C dans le plan équatorial pour une valeur nulle de l'équation du temps.
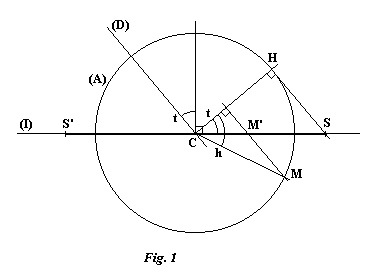
L'intersection du plan de l'équateur et de la table du cadran est représentée
par la droite (I). (D) est la direction de projection choisie et SS' le segment
correspondant à la projection du cercle auxiliaire. Soit H le point horaire
du cercle projeté en S et t l'angle HCS; t est aussi l'angle que fait
la droite (D) avec la perpendiculaire à (I). On remarquera que l'angle
CHS est droit. En choisissant la longueur s = CS du demi-segment SS' on impose
donc le rayon r0 = s.cos t au cercle auxiliaire. La projection d'un point horaire
quelconque M du cercle distant de H de l'angle MCH = h donne le point M' appartenant
au segment SS'. La distance de M' à C est:
M'C
= r0.cos h / cos t
M'C = s.cos h
Elle
est négative quand M' est situé entre S' et C.
L'axe du monde est perpendiculaire au plan de la figure et passe par C. Le point
efficace P du cadran auxiliaire est situé sur cet axe à la distance
PC de C telle que:
PC
= r0.tg d0
PC = s.cos t.tg d0
d0
étant la déclinaison du soleil pour la date particulière
où l'équation du temps est nulle. Le style doit alors être
positionné passant par P et parallèle à (D).
Pour une valeur E de l'équation du temps, lorsque le cercle (A) a été
tourné de cette valeur, le moyen de retrouver la même projection
SS' est de tourner également du même angle la direction de projection
de façon à conserver la perpendicularité avec CH (voir
figure 2).
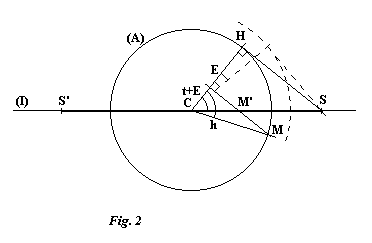
Le rayon du cercle auxiliaire doit alors être ajusté à la valeur r = s.cos (t + E) et on retrouve bien que M', projection du point horaire M, est distant de C de la valeur:
M'C
= r.cos h / cos (t + E)
M'C = s.cos h
Quant
au style, il doit être déplacé sur l'axe du monde à
la distance PC = s.cos (t + E).tg d, d étant la déclinaison du
soleil, puis tourné de l'angle E pour se retrouver parallèle à
HS.
Dans la pratique, la réalisation d'un tel cadran est problématique
en ce qui concerne le positionnement du style. Le support idéal est bien
sûr l'axe du monde car le style s'appuie toujours sur lui et il lui est
toujours perpendiculaire. Cependant, pour un plan de cadran quelconque, l'axe
polaire n'est accessible au dessus de la table du cadran que pour une moitié
des déclinaisons du soleil. Il reste toutefois la possibilité
que l'axe polaire appartienne au plan du cadran, ce qui est le cas, par exemple,
pour le cadran de Parent. On peut alors imaginer un système d'indexation
qui donne au style la bonne orientation en fonction de son déplacement
sur l'axe du monde.
Une autre difficulté, inhérente à ce type de cadran, est qu'à un même point du segment SS' correspondent deux heures différentes et qu'il n'y a pas de règle simple qui indique quelle heure il faut lire.
Finalement, en guise de résumé, voyons comment modifier un cadran de Parent pour qu'il indique l'heure légale. Il faut, à partir de sa position d'origine:
Faire
tourner le style autour de l'axe du monde de l'angle a exprimé en degré:
a = lo + 15.fh + E/4
avec:
lo: Longitude du lieu où est situé le cadran, exprimée
en degré et positive à l'ouest du méridien de Greenwich
fh: Fuseau horaire exprimé en heure
E: Equation du temps exprimée en mn et correspondant à l'avance
du temps moyen sur le temps vrai
Lorsque a est positif on doit faire tourner le style dans le sens trigonométrique
en le regardant du pôle nord.
Diminuer la distance du style à la ligne équatoriale, en multipliant
cette distance par le facteur f:
f = cos (lo + 15.fh + E/4)
|
Recherche-Web |
 |
 |
 |
 |
 |